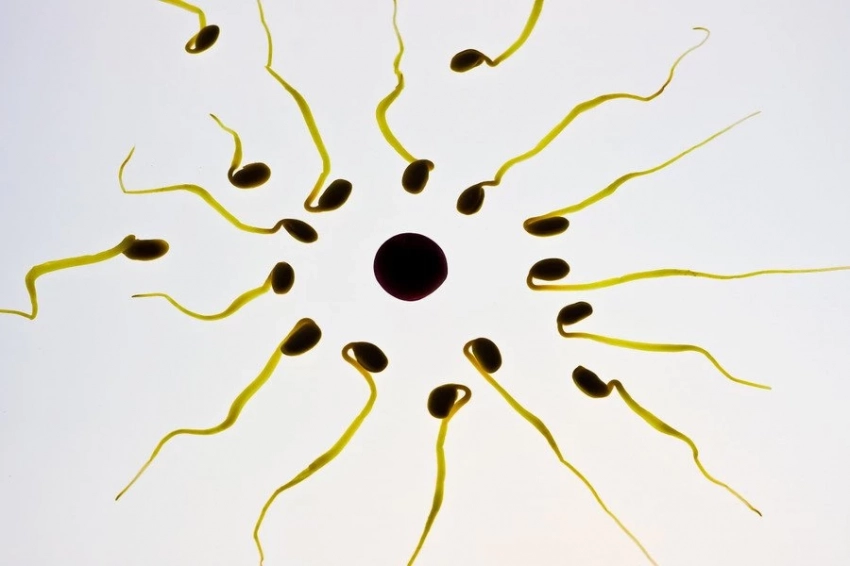
Движения хвоста сперматозоида объяснили математическим принципом Алана Тьюринга

Ученые из Великобритании доказали, что жгутик сперматозоида движется по траектории, принцип, который описал Алан Тьюринг больше 70 лет назад для узоров, встречающихся в природе.

 

Алан Тьюринг — британский математик и криптограф, основоположник теоретической информатики и теории искусственного интеллекта. Во время Второй мировой войны его теории помогли взломать код «Энигмы», немецкой шифровальной аналоговой машины.

 

В 1950-е годы им же была выдвинута гипотеза, описывающая замысловатые узоры на теле животных. Они формируются благодаря неоднородностям в исходной гомогенной смеси веществ. Столь сложные паттерны являются результатом распространения (диффузии) химических соединений и их взаимодействия. Гипотезе дали название «реакционно-диффузионная теория» или «паттерны Тьюринга». Она распространяется и на другие виды макроскопических природных структур.

 

Публикация в журнале Nature Communications рассказала о работе ученых из британского Бристольского университета, которые попытались выяснить, есть ли связь между создающими узоры химическими закономерностями и тем, как движутся хвосты сперматозоидов.

 

Жидкая среда, в которой сперматозоиды движутся, создает сопротивление. Его изучили исследователи с помощью компьютерной модели. Оказалось, что семенная жидкость мало влияет на движение и форму жгутика. Получается, что «волнистость» их движений возникает без этого воздействия.

 

Оказалось, что движения жгутика возникают ровно так же, как и узоры, описанные моделью Тьюринга. «Узоры» жгутиков возникают под действием двух основных факторов. Первая — внутренняя, это химические реакции, приводящие в действие моторные белки.

 

Вторая — изгибающее движение эластичного жгутика, которое стремится к равновесию. То есть, сгибательные и колебательные движения идут вдоль хвостика, примерно так же, как капля красителя движется в жидкости, пока цвет не становится равномерным. Именно такую модель и описывает математика Тьюринга.

 

Природные процессы наверняка более сложные, не умещаются ровно в математические алгоритмы. Но полученные данные помогут решать реальные проблемы, например, с фертильностью, обусловленной аномальным движение жгутиков. А еще они позволят создавать искусственные мышцы и «одушевленные материалы», обладающие свойствами живых организмов.